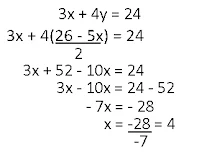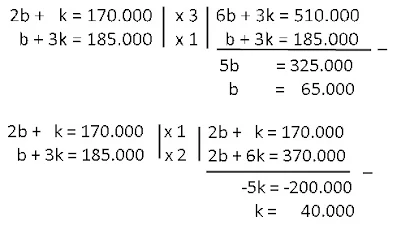Soal Latihan Fluida Statis Dan Pembahasan Bimbel Jakarta Timur
| Fluida Statis atau hidrostatika ini membahas tentang karakteristik seperti tekanan dan gaya pada fluida yang tidak bergerak. Zat yang termasuk dalam pembahasan fluida adalah Zat cair dan gas.Berikut adalah soal-soal latihan untuk membantu lebih memahami tentang fluida statis.
1. Besarnya tekanan hidrostatik ditentukan oleh ....
a. volume dan kedalaman zat cairb. massa jenis zat cair dan kedalaman zat cair
c. massa jenis zat cair, volume dan kedalaman zat cair
d. massa jenis zat cair, percepatan gravitasi dan kedalaman zat cair
Pembahasan :
Ph=⍴ . g . h
⍴= massa jenis zat cair
g=percepatan gravitasi
h=kedalaman zat cair
Jawaban : d
2. Gaya ke atas yang bekerja pada sebuah benda di dalam zat cair sebanding dengan ....
a. berat bendab. massa jenis zat cair dan berat benda
c. massa jenis zat cair dan volume benda yang tercelup
d. massa jenis benda dan volume benda seluruhnya
Pembahasan :
Gaya ke atas besarnya adalah hasil kali massa jenis fluida, percepatan gravitasi dan volume benda yang tercelup dalam fluid
Fa= =⍴. g. V
Jawaban : c
3.Sebuah bejana berisi air setinggi 100 cm. Jika percepatan gravitasi 10 m/s², maka besar tekanan hidrostatis pada dasar bejana adalah....
a. 10³ N/m²b. 10⁴ N/m²
c. 10⁵ N/m²
d. 10⁶ N/m²
Pembahasan :
Diketahui : ⍴air=1000 kg/m³
g = 10 m/s²
h =100 cm=1 m
Ditanya=Ph ?
Jawab : Ph=⍴ . g. h
Ph=1000. 10. 1
= 10⁴ N/m²
Jawaban : b
4. Bongkahan es terapung di atas permukaan laut dengan setengah bagian yang muncul di permukaan. Jika massa jenis air laut 1,03 g/cm³ dan volume seluruh es adalah 1 m³, besar gaya ke atas es tersebut adalah....
a. 2.575 Nb. 5.150 N
c. 7.725 N
d. 10.300 N
Pembahasan :
Diketahui : ⍴=1,03 g/cm³=1.030 kg/m³
g=10 m/s² (jika dalam soal tidak diketahui maka gunakan nilai ini)
V=½ x 1 m³ (volum benda yang tercelup)
=0,5 m³
Ditanya Fa?
Jawab : Fa=⍴. g. V
=1.030 . 10. 0,5
= 5.150 N
Jawaban : b
5. Suatu bejana berhubungan berbentuk U, diisi air pada salah satu kakinya. Pada kaki yang lain diisi minyak yang massa jenisnya 800 kg/m³. Jika tinggi minyak dari bidang batas air-minyak adalah 10 cm, maka perbedaan tinggi air adalah....
a. 4 cmb. 6 cm
c. 8 cm
d. 12 cm
Pembahasan :
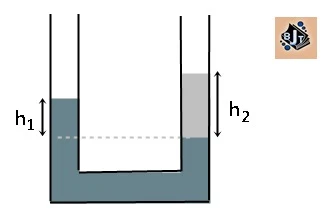 |
| Gambar 1 |
Diketahui :⍴₁=⍴air =1000 kg/m³
⍴₂=⍴myk= 800 kg/m³
h₂=hmyk= 10 cm
Ditanya : h₁?
Jawab : ⍴₁ . h₁= ⍴₂ . h₂
1000 . h₁=800. 10
1000 . h₁=8000
h₁=8000 : 1000
h₁=8 cm
Jawaban : c
6. Kempa hidrolik memiliki perbandingan diameter pengisap 1 : 5. Apabila pada pengisap besar diberi beban 30.000 N, maka berapa besar gaya yang harus diberikan pada pengisap kecil agar seimbang?
a. 8 Nb 12 N
c 16 N
d. 20 N
Pembahasan :
Diketahui :D₁ : D₂=1 : 50, sehingga
A₁ : A₂=(D₁ : D₂)²=1: 2.500
F₂ =30.000 N
Ditanya F₁ ?
Jawab :
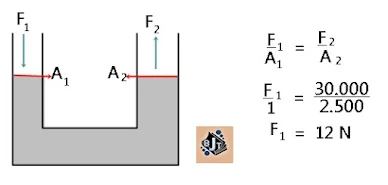 |
| Gambar 2 |
Jawaban : b
7. Pada torak kecil sebuah pompa hidrolik diberi beban sebesar 100 N. Jika luas permukaan torak kecil 10 cm², agar torak besar menghasilkan gaya 1.000 N, luas penampang torak besar harus....
a. 10 cm²b. 20 cm²
c. 50 cm²
d. 100 cm²
Pembahasan :
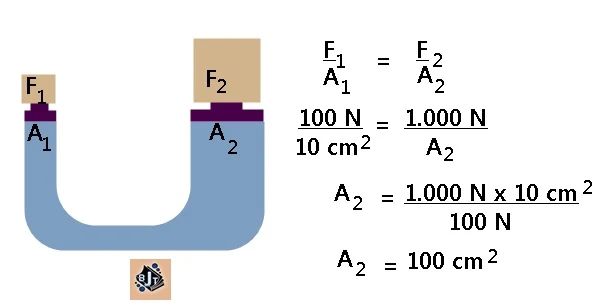 |
| Gambar 3 |
Jawaban : d
8.Sebuah benda terapung di atas zat cair dengan 3/4 bagian benda tercelup ke dalam zat cair. Jika massa jenis benda adalah 0,6 gr/cm³, berapa massa jenis zat cair?
a.0,8 g/cm³b.0,75 g/cm³
c.0,4 g/cm³
d.0,3 g/cm³
Pembahasan :
Diketahui : Vc=3/4 Vb
⍴b=0,6 gr/cm³
Ditanya ⍴c ?
jawab : Benda yang terapung memiliki gaya ke atas sama dengan berat benda
Fa=W
⍴c. Vc. g= ⍴b. Vb. g............ (kedua ruas bagi dengan g)
⍴c.3/4 Vb= 0,6 gr/cm³. Vb.....(kedua ruas bagi dengan Vb)
⍴c=0,6 : 3/4
⍴c=0,8 g/cm³
Jawaban : a
9. Sebuah balok kayu yang massa jenisnya 0,75 gr/cm³ terapung di atas air yang massa jenisnya 1 gr/cm³. Jika volume balok 12 cm³, volume balok yang tercelup di dalam air adalah....
a. 1 cm³b. 3 cm³
c. 5 cm³
d. 9 cm³
Pembahasan :
Diketahui : ⍴b= 0,75 gr/cm³
⍴c=1 g/cm³
Vb=12 cm³
Ditanya Vc?
Jawab : Fa=W
⍴c. Vc. g= ⍴b. Vb. g
⍴c. Vc = ⍴b. Vb
1 . Vc =0,75 . 12
Vc =9 cm³
Jawaban : d
10. Serangga dapat berjalan pada permukaan air, karena....
a. berat jenis serangga lebih kecil daripada air
b. berat jenis serangga lebih besar daripada air
c. gaya apung archimedes
d. tegangan permukaan air
Pembahasan :
Adanya gaya atau tarikan ke bawah yang menyebabkan permukaan cairan berkontraksi dan benda dalam keadaan tegang. Gaya ini disebut tegangan permukaan air. Serangga yang hinggap di permukaan air tidak tenggelam karena gaya berat serangga masih lebih kecil dibandingkan dengan tegangan permukaan air, sehingga serangga masih bisa ditahan oleh gaya atau tegangan permukaan air.
Jawaban : d
11. Sebuah pipa kapiler berdiameter 0,4 mm dicelupkan ke dalam air yang massa jenisnya 1.000 kg/m³. Tegangan permukaan air yang dialami adalah 10⁻²N/m dan sudut kontak 30⁰. Jika g=10 m/s², maka kenaikan air dalam pipa kapiler adalah....
a.8,5 mm
b.17 mm
c.8,5 cm
d. 17 cm
Pembahasan :
Diketahui : r=d/2=0,4 mm/2=0,2 mm=0,2 . 10⁻³ m
⍴=1.000 kg/m³
θ= 30⁰
Ɣ= 10⁻²N/m
g=10 m/s²
Ditanya : y ?
Jawab : y= 2 Ɣ cos θ
⍴ g r
= 2.10⁻².cos 30⁰
1.000.10.0,2.10⁻³
=0,85 .10⁻² m
=8,5 mm
Jawaban : a
12. Untuk mengangkat sebuah mobil yang massanya 4 ton, dipergunakan pompa hidrolik. Jika perbandingan diameter penghisap kecil dan besar 1 : 40, maka gaya yang diperlukan pada penghisap kecil adalah....
a. 2,5 Nb. 10 N
c. 25 N
d. 50 N
Pembahasan :
Diketahui : m=4 ton=4.000 kg
D₁ : D₂ =1 : 40
Ditanya : F?
Jawab : W=m.g=4.000 x 10=40.000 N
A₁ : A₂ =(D₁ : D₂)²
=(1 : 40)²=1 : 1.600
 |
| Gambar 4 |
13. Jika percepatan gravitasi 10 m/s² dan massa jenis raksa adalah 13,6 gr/cm³, maka berat jenis raksa dalam sistem SI adalah....
a. 13,6 N/m³b. 13,6 x 10² N/m³
c. 13,6 x 10³ N/m³
d. 13,6 x 10⁴ N/m³
Pembahasan :
Diketahui : g=10 m/s²
⍴= 13,6 gr/cm³=13.600 kg/m³
Ditanya : Bj?
Jawab : Bj=⍴ x g
= 13.600 x 10
=136.000
=13,6 x 10⁴ N/m³
Jawaban : d
14. Kubus perak memiliki volume 125 cm³. Saat ditimbang di udara beratnya 10 N. Saat dicelupkan seluruhnya ke dalam minyak, ternyata beratnya menjadi 9 N. Besar massa jenis minyak adalah....
a. 0,8 kg/m³b. 8 kg/m³
c. 80 kg/m³
d. 800 kg/m³
Pembahasan :
Diketahui : V =125 cm³=125 x 10⁻⁶ m³
Wu=10 N
Wf =9 N
Ditanya=⍴f ?
Jawab : Fa=Wu - wf
⍴f. V.g=10 - 9
⍴f.125 x 10⁻⁶ .10=1
⍴f.125 x 10⁻⁵ =1
⍴f=10⁵:125
= 800 kg/m³
Jawaban : d
15. Alat berikut yang merupakan penerapan hukum Pascal adalah...
a. water passb. pompa hidrolik
c. galangan kapal
d. balon udara
Pembahasan :
- water pass=hukum bejana berhubungan
- pompa hidrolik=hukum Pascal
- galangan kapal=hukum Archimedes
- balon udara=hukum Archimedes
Jawaban : b
16. Sebuah benda ketika ditimbang di udara beratnya 15 N. Jika volume benda 1.000 cm³ dan benda dicelupkan ke dalam air, maka beratnya di dalam air adalah....
a. 10 Nb. 7,5 N
c. 6 N
d. 5 N
Pembahasan :
Diketahui : Wu=15 N
V =1.000 cm³=10⁻³ m³
⍴a=1.000 kg/m³
Ditanya : Wa ?
Jawab : Fa=Wu - Wa
⍴a. V.g= Wu - Wa
1.000 x 10⁻³ x 10=15 - Wa
10=15 - Wa
Wa=15 - 10=5 N
Jawaban : d
17. Sebuah tabung yang tingginya 1 m diisi penuh air dan minyak. Jika massa jenis air 1 gr/cm³ dan minyak 0,9 gr/cm³, berapakah perbandingan tinggi air dan minyak agar tekanan hidrostatik di dasar tabung besarnya 9,6 x 10³ pascal ?
a. 3 : 2b. 2 : 3
c. 4 : 1
d. 1 : 4
Pembahasan :
 |
| Gambar 5 |
Diketahui : ⍴₁= 1 gr/cm³=1.000 kg/m³
⍴₂=0,9 gr/cm³=900 kg/m³
h₁ + h₂=1 m
h₁=1 - h₂
Ph= 9,6 x 10³ pascal
Ditanya : h₁ : h₂ ?
Jawab : Ph=P₁ + P₂
9,6x 10³= ⍴₁.g.h₁ + ⍴₂.g.h₂
9,6x 10³=1.000 x 10 x h₁ + 900 x 10 x h₂
9,6x 10³=10 x 10³x h₁ + 9 x 10³x h₂
9,6=10 h₁ + 9 h₂
substitusi h₁=1 - h₂
9,6=10 (1 - h₂) + 9 h₂
9,6=10 - 10h₂ + 9h₂
9,6=10 - h₂
h₂=10 - 9,6=0,4 m
h₁=1 - h₂
=0,6 m
h₁ : h₂=0,6 : 0,4=3 : 2
Jawaban : a
18. Tekanan udara di kaki sebuah gunung adalah 760mmHg, dan di puncaknya adalah 608 mmHg. Jika massa jenis udara adalah 1,25 kg/m³, massa jenis raksa 13.600 kg/m³, dan percepatan gravitasi 10 m/s² (1 atm=1,01 x 10⁵ Pa) maka tinggi gunung tersebut adalah...
a.13.600 mb.1.616 m
c.608 m
d.152 m
Pembahasan :
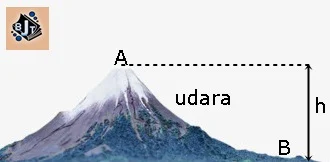 |
| Gambar 6 |
PB= 760mmHg
= 1,01 x 10⁵ Pa
⍴u= 1,25 kg/m³
⍴r= 13.600 kg/m³
Ditanya hA ?
Jawab :
PB - PA= 760 mmHg - 608 mmHg
=152 mmHg
=152 x 1,01 x 10⁵
760
=2,02 x 10⁴ Pa
Tekanan pada titik B ( di kaki gunung) dipengaruhi oleh tekanan luar di titik A dan tekanan hidrostatik.
PB=PA + Ph
PB - PA= ⍴u.g.h
h= PA - PB
⍴u.g
= 2,02 x 10⁴
1,25 . 10
=1.616 m
Jawaban : b
19. Sepotong kawat yang panjangnya 16 cm dicelupkan secara horisontal ke dalam cairan alkohol. Jika kawat diangkat keluar dari alkohol, timbul gaya sebesar 7,68 N akibat tegangan permukaan. Besar tegangan permukaan alkohol adalah....
a. 48 N/mb. 36 N/m
c. 24 N/m
d. 12 N/m
Pembahasan :
Diketahui : L=16 cm=16 x 10⁻²m
F=7,68 N
Ditanya Ɣ ?
Jawab : Ɣ= F
2.L
= 7,68
2. 16 x 10⁻²
=24 N/m
Jawaban : c
20. Sebuah pipa kapiler dengan diameter 0,4 mm dimasukkan tegak lurus ke dalam bejana yang berisi raksa. Jika sudut kontak raksa dengan dinding 120° dan tegangan permukaan 0,68 N/m, aksa akan turun dalam pipa sebesar....
a. 25 cmb. 12,5 cm
c. 2,5 cm
d. 1,25 cm
Pembahasan :
Diketahui : d=0,4 mm=4 x 10⁻⁴m
r=d/2=2 x 10⁻⁴m
θ= 120°
Ɣ=0,68 N/m
⍴=13.600 kg/m³
Ditanya y ?
Jawab : y= 2.Ɣ. cos θ
⍴.g.r
= 2.0,68.cos 120°
13.600 x 10 x 2 x 10⁻⁴
= 1,36 . -0,5
27,2
=- 0,025 m
=- 2,5 cm (Nilai negatif menunjukkan penurunan)
Jawaban : c
Demikian soal-soal latihan materi Fluida Statis berikut pembahasannya. Semoga bermanfaat dan dapat membantu anda lebih memahami materi yang diberikan. Jika ada masukan dan koreksi, silahkan tulis komentar. Selanjutnya kamu juga dapat berlatih Soal Fluida Dinamis.
Penelusuran :
soal pilihan ganda fluida statis dan jawabannya
5 contoh soal fluida statis
contoh soal fluida statis beserta jawabannya
soal fluida statis pdf
contoh soal fluida statis brainly
soal fluida statis dan dinamis doc
contoh soal dan pembahasan fluida statis pdf
soal fluida statis doc
https://www.radarhot.com/2018/11/soal-latihan-fluida-statis-dan.html
Sistem Persamaan Linear Dua Variabel By Bimbel Jakarta Timur
Sistem persamaan linear dua variabel by Bimbel jakarta Timur, yang di pelajari kelas 8 sering kita gunakan untuk materi lain baik dalam pelajaran matematika, juga pada pelajaran lain seperti fisika, ekonomi dan lainnya. Sistem persamaan linear dua variabel, tiga variabel digunakan untuk menentukan solusi suatu persamaan
Sistem persamaan linear adalah sekumpulanpersamaan linear (garis lurus) yang terdiri dari beberapa variabel yang dari sistem tersebutdapat ditentukan nilai dari variabel yang diberikan.Apa sih variabel itu? Variabel atau peubah adalahlambang pengganti suatu bilangan yang belum diketahui nilainya dengan pasti. Nahhhpada sistem persamaan ini kita dapat mengetahui nilai variabel yang diberikan.Bagaimana caranya? Ada beberapa cara yang bisa digunakan untuk mencari nilai ataupenyelesaian sistem persamaan linear dua variabel.
1. Metode grafik
Cara inidilakukan dengan menggambar masing-masing persamaan yang diberikan pada diagramkartesius hingga ditemukan sebuah titik potong. Titik potong yang didapat ituadalah penyelesaian sistem persamaan tersebut.
Contoh :
Tentukanhimpunan penyelesaian dari sistem persamaan linear berikut :
a. x + y=6 dan 2x + y=8
b. 3x + 2y=12 dan x + 2y=8
Jawab :
a. Untuk menggambar grafik persamaan linear, kita harus mencari titik potong garis terhadap sumbu x dan sumbu y. Titik potong garis terhadap sumbu x didapat jika nilai y=0, sebaliknya titik potong terhadap sumbu y didapat jika nilai x=0. Setelah didapatkan dua titik potong tersebut maka dapat ditarik garis yang melewati kedua titik.
Garis x + y=6
Titik potong sumbu x ( y=0)
x + 0=6
x=6
titik potong (6,0)
Titik potong sumbu y (x=0)
0 + y=6
y=6
titik potong (0,6)
Tarik garis yang melewati kedua titik maka didapatkan garis seperti yg tergambar dengan garis warna biru pada diagram kartesius di bawah.
Garis 2x + y=8
Titik potong sumbu x ( y=0)
2x + 0=8
2x=8
x=4
titik potong (4,0)
Titik potong sumbu y (x=0)
2(0) + y=8
y=8
titik potong (0,8)
Tarik garis yang melewati kedua titik maka didapatkan garis seperti yg tergambar dengan garis warna merah pada diagram kartesius di bawah.
 |
| SPLDV Metode Grafik |
Kedua garis yang telah digambar berpotongan pada titik (2,4). Maka penyelesaian dari sistem persamaan linear tersebut adalah (2,4) yang artinya nilai x=2 dan nilai y=4.
b. Garis 3x + 2y=12
Titik potong sumbu x ( y=0)
3x + 2(0)=12
3x=12
x=4
titik potong (4,0)
Titik potong sumbu y (x=0)
3(0) + 2y=12
2y=12
y=6
titik potong (0,6)
Pada gambar di bawah ditunjukkan dengan garis biru
Garis x + 2y=8
Titik potong sumbu x ( y=0)
x + 2(0)=8
x=8
titik potong (8,0)
Titik potong sumbu y (x=0)
0 + 2y=8
2y=8
y=4
titik potong (0,4)
Pada gambar dibawah ditunjukkan dengan garis merah
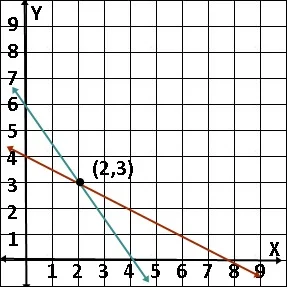 |
| SPLDV Metode Grafik |
Kedua garis yang telah digambar berpotongan pada titik (2,3). Maka penyelesaian dari sistem persamaan linear tersebut adalah (2,3) yang artinya nilai x=2 dan nilai y=3.
2. Metode Substitusi
Metode Substitusi adalah suatu metode mencari penyelesaian persamaan dengan cara mensubstitusi (mengganti) salah satu variabelnya dengan persamaan lain ataupun dengan nilai yang sudah diketahui.
contoh :
a. 3x + y=0 dan 2x – 3y=11
b. 4x + 3y=6 dan 2x – y=3
c. 3x+ 4y=24 dan 5x + 2y=26
Jawab :
a. Pilih salah satu persamaan yang akan kita substitusi ke persamaan lain. Lalu ubah salah satu variabelnya menjadi bentuk persamaan ekuivalen.
Kita pilih persamaan 3x + y=0
Ubah dengan memindahkan 3x ke ruas kanan sehingga bentuknya menjadi
y=- 3x
Substitusi nilai y ke persamaan yang lain
2x - 3y=11
2x - 3 (-3x)=11
2x + 9x=11
11x=11
x=1
Substitusi nilai x ke salah satu persamaan yang kita inginkan
2x - 3y=11
2(1) - 3y=11
2 - 3y=11
- 3y=11 - 2
- 3y=9
y=9/-3
y=-3
Penyelesaian (1,-3)
b. 4x + 3y=6 dan 2x – y=3
Misalkan dipilih 2x - y=3
2x - y=3
- y=3 - 2x
y=2x - 3
Substitusi ke persamaan 4x + 3y=6
4x + 3(2x - 3)=6
4x + 6x - 9=6
10x=6 + 9
10x=15
x=15/10=1½
Substitusi nilai x ke salah satu persamaan
2x - y=3
2(1½) - y=3
3 - y=3
- y=3 - 3
- y=0
y=0
Penyelesaian (1½, 0)
Substitusi nilai x ke salah satu persamaan
5x + 2y=26
5(4) + 2y=26
20 + 2y=26
2y=26 - 20
2y=6
y=6/3=2
Penyelesaiannya adalah (4,2)
Maka harga 1 baju adalah Rp 65.000,00 dan harga 1 kaos Rp 40.000,00.
Harga 3 baju dan 2 kaos adalah
3b + 2k=3(65.000) + 2 (40.000)
=195.000 + 80.000
=Rp 275.000,00
3. Keliling sebuah persegi panjang sama dengan 44 cm. Jika lebarnya 6 cm lebih pendek dari panjangnya, Tentukan luas dari persegi panjang tersebut.
Jawab :
Rumus keliling=2 (p + l)=2p + 2l, maka
2p + 2l=44
p - l=6 ⇒ p=6 + l
2p + 2l=44
2(6 + l) + 2l=44
12 + 2l + 2l=44
4l=44 -12
4l=32
l=8 cm
p=6 + l
p=6 + 8=14 cm
Luas=p x l
=14 cm x 8 cm
=112 cm²
Jumlah risol yang dijual adalah 16 buah dan bolu 24 buah.
Keuntungan yang diperoleh adalah
500a + 500b=400(16) + 500(24)
=6.400 + 12.000
=Rp 18.400,00
Demikian materi Sistem Persamaan Linear Dua Variabel dan berberapa contoh soal serta pembahasan yang diberikan Bimbel Diah Jakarta Timur. Semoga dapat membantu untuk lebih memahami.
5x + 2y=26
5(4) + 2y=26
20 + 2y=26
2y=26 - 20
2y=6
y=6/3=2
Penyelesaiannya adalah (4,2)
3. Metode Eliminasi
Metode Eliminasi adalah suatu metode mencari penyelesaian persamaan dengan cara mengeliminasi (menghilangkan) salah satu variabelnya. Menghilangkan variabel adalah dengan cara menyamakan koefisien variabel yang dipilih terlebih dahulu.
contoh :
a. 4x - 5y=-9 dan 2x + 3y=23
b. 4x - 3y=15 dan -3x + 2y=- 12
Jawab
a. Jika ingin mengeliminasi variabel x maka samakan koefisien variabel x menjadi KPK dari kedua koefisien.
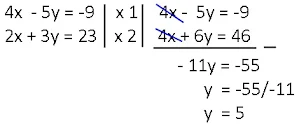 |
| penyelesaian |
Jika koefisien variabel yang dieliminasi bertanda sama (sama-sama negatif atau sama-sama negatif), maka eliminasi dengan cara mengurangi. Tetapi jika koefisien variabel yang ingin dieliminasi berbeda, maka eliminasi dengan cara menjumlah.
 |
| penyelesaian |
Penyelesaiannya adalah (4,5)
b. Eliminasi variabel x
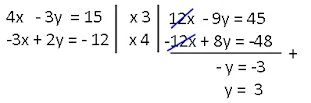 |
| penyelesaian |
Eliminasi variabel y
 |
| penyelesaian |
Penyelesaiannya adalah (6,3)
4. Metode Eliminasi dan Substitusi
Metode berikut menggunakan eliminasi untuk mendapatkan nilai dari salah satu variabel. Kemudian variabel yang sudah diketahui nilainya disubstitusi ke salah satu persamaan untuk mendapatkan nilai variabel yang lain.
contoh :
Tentukan himpunan penyelesaian sistem persamaan
2x +3y=12 dan 4x -7y=-2
Jawab :
Eliminasi variabel x
 |
| penyelesaian |
Substitusi nilai y ke persamaan 2x + 3y=12
2x + 3(2)=12
2x + 6 =12
2x =12 -6
2x =6
x =6/2=3
Himpunan penyelesaian{(3,2)}
Selain metode-metode penyelesaian di atas, ada beberapa model sistem persamaan linear yang membutuhkan penyelesaian tambahan. Perhatikan beberapa contoh sistem persamaan berikut, tentukan himpunan penyelesaiannya.
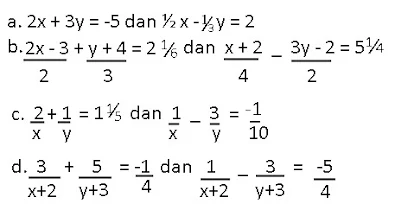 |
| penyelesaian |
Jawab
a. Persamaan kedua berupa pecahan, agar lebih mudah maka kedua ruas dikali dengan KPK penyebutnya agar koefisien variabel berupa bilangan bulat.
½x - ⅓ y=2......... dikali 6
3x - 2y=12
Lanjutkan penyelesaian dengan metode yg telah dibahas sebelumnya, misalnya metode eliminasi.
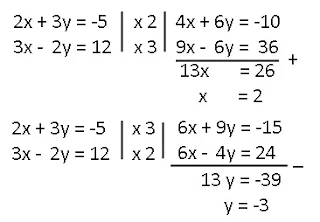 |
| penyelesaian |
Himpunan penyelesaian{(2, -3)}
b. Persamaan pertama dikali 6
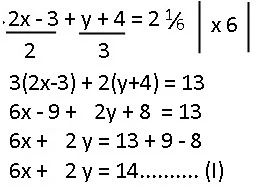 |
| penyelesaian |
Persamaan kedua dikali 4
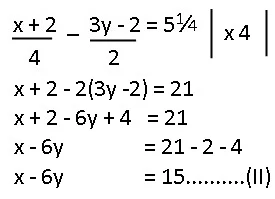 |
| penyelesaian |
Lanjutkan penyelesaian dari (I) dan (II)
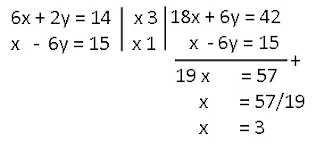 |
| penyelesaian |
x - 6y=15
3 - 6y=15
- 6y=15 -3
- 6y=12
y=12/-6
y=-2
Himpunan penyelesaian{(3,-2)}
c. Misalkan a=1/x dan b=1/y, maka
persamaan I menjadi 2a + b=6/5
persamaan II menjadi a - 3b=-1/10 → a=3b - 1/10
Substitusi ke 2a + b=6/5
2(3b - 1/10) + b=6/5
6b - 1/5 + b =6/5
6b + b =6/5 + 1/5
7b =7/5
b =1/5
1/y =1/5, maka y=5
a=3b - 1/10
a=3(1/5) - 1/10
a=3/5 - 1/10
a=5/10
a=1/2
1/x=1/2
x =2
Himpunan penyelesaian{(2,5)}
d. Misalkan a=1/(x+2), b=1/(y+3) maka
3a + 5b=-1/4
a - 3b=-5/4 → a=3b - 5/4
Substitusi ke 3a + 5b=-1/4
3(3b - 5/4) + 5b=-1/4
9b -15/4 + 5b =-1/4
9b + 5b =-1/4 + 15/4
14b =14/4
b =1/4
1/(y+3) =1/4
y+3 =4
y =4 - 3=1
a=3b - 5/4
a=3(1/4) - 5/4
a=3/4 - 5/4
a=-2/4
a=-1/2
1/(x+2)=-1/2
x + 2 =-2
x =-2 - 2
x =-4
Himpunan penyelesaian{(-4,1)}
Contoh soal cerita
1. Harga3 pensil dan 2 buku tulis adalah Rp5.100,00. Sedangkan harga 2 pensil dan 4buku tulis adalah Rp7.400,00. Model matematika yang tepat untuk pernyataantersebut adalah….
Jawab :
Misalkan hal yang diketahui menjadi variabel yang sesuai, misalnya x dan y, a dan b, p dan q dan sebagainya. Untuk menjawab soal ini kita misalkan pensil dengan p dan buku dengan b.
3 pensil dan 2 buku tulis adalah Rp5.100,00
⇒3p + 2b=5.100
2 pensil dan 4 buku tulis adalah Rp7.400,00
⇒ 2p + 4b=7.400
bisa disederhanakan dengan sama-sama dibagi 2
⇒ p + 2b=3.700
Jawab :
Misalkan hal yang diketahui menjadi variabel yang sesuai, misalnya x dan y, a dan b, p dan q dan sebagainya. Untuk menjawab soal ini kita misalkan pensil dengan p dan buku dengan b.
3 pensil dan 2 buku tulis adalah Rp5.100,00
⇒3p + 2b=5.100
2 pensil dan 4 buku tulis adalah Rp7.400,00
⇒ 2p + 4b=7.400
bisa disederhanakan dengan sama-sama dibagi 2
⇒ p + 2b=3.700
2. Jika harga2 buah baju dan 1 kaos adalah Rp.170.000,00. Sedangkan harga 1 baju dan 3 kaos adalahRp.185.000,00. Harga 3 baju dan 2 kaos adalah.....
Jawab :
Misalkan baju=b dan kaos=k
Sistem persamaan linear :
2b + k=170.000
b + 3k=185.000
Jawab :
Misalkan baju=b dan kaos=k
Sistem persamaan linear :
2b + k=170.000
b + 3k=185.000
Maka harga 1 baju adalah Rp 65.000,00 dan harga 1 kaos Rp 40.000,00.
Harga 3 baju dan 2 kaos adalah
3b + 2k=3(65.000) + 2 (40.000)
=195.000 + 80.000
=Rp 275.000,00
3. Keliling sebuah persegi panjang sama dengan 44 cm. Jika lebarnya 6 cm lebih pendek dari panjangnya, Tentukan luas dari persegi panjang tersebut.
Jawab :
Rumus keliling=2 (p + l)=2p + 2l, maka
2p + 2l=44
p - l=6 ⇒ p=6 + l
2p + 2l=44
2(6 + l) + 2l=44
12 + 2l + 2l=44
4l=44 -12
4l=32
l=8 cm
p=6 + l
p=6 + 8=14 cm
Luas=p x l
=14 cm x 8 cm
=112 cm²
4.Bibi menjual dua jenis kue yaitu risol dan bolu. Keranjang berdagangnya hanya dapatmemuat 40 buah kue. Harga modal risol adalah RP 1.500,00 perbuah, sedangkanharga modal bolu adalah Rp 2.000,00. Modal yang ia keluarkan adalah Rp72.000,00. Berapa pendapatan Bibi jika penjualan risol untungnya Rp 400,00 perbuah dan bolu memberikan untung Rp 500,00 perbuah?
Jawab :
Misalkan risol=a dan bolu=b
jumlah kue=40 ⇒ a + b=40
modal kue ⇒ 1.500a + 2.000b=72.000 (sederhanakan dengan dibagi 500)
⇒ 3a + 4b=144
Jawab :
Misalkan risol=a dan bolu=b
jumlah kue=40 ⇒ a + b=40
modal kue ⇒ 1.500a + 2.000b=72.000 (sederhanakan dengan dibagi 500)
⇒ 3a + 4b=144
Keuntungan yang diperoleh adalah
500a + 500b=400(16) + 500(24)
=6.400 + 12.000
=Rp 18.400,00
Demikian materi Sistem Persamaan Linear Dua Variabel dan berberapa contoh soal serta pembahasan yang diberikan Bimbel Diah Jakarta Timur. Semoga dapat membantu untuk lebih memahami.