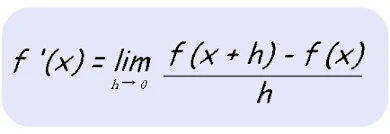STOIKIOMETRI by Bimbel Jakarta Timur
Dalam Artikel ini Bimbel Jakarta Timur akan membahas secara Khusus mengenai Stoikiometri yaitu cabang ilmu kimia yang mempelajari dan menghitung hubungan kuantitatif antara pereaksi (reaktan) dan hasil reaksi (produk) dalam persamaan kimia.
Hukum-hukum Dasar Kimia
1. Hukum kekekalan massa (hukum Lavoisier) : massa total zat-zat sebelum reaksi akan selalu sama dengan massa total zat-zat setelah reaksi.
contoh : 3 gram gas hidrogen(H2) yang bereaksi dengan 24 gram gas oksigen (O2) akan membentuk 27 gram air (H2O)
2. Hukum perbandingan tetap (hukum Proust) : perbandingan massa unsur dalam senyawa selalu tetap.
contoh :
H2 | O2 | H2O | Keterangan |
1 gram | 8 gram | 9 gram | |
2 gram | 8 gram | 9 gram | sisa H2=1 gram |
2 gram | 17 gram | 18 gram | sisa O2=1 gram |
4 gram | 25 gram | 27 gram | sisa H2=1 gram, O2=1 gram |
3. Hukum perbandingan berganda ( hukum Dalton) : jika dua unsur dapat membentuk lebih dari satu senyawa dan massa salah satu unsur tersebut tetap(sama), perbandingan massa unsur yang lain dalam senyawa tersebut merupakan bilangan bulat sederhana.
contoh :
Perbandingan H : O dalam H2O =2 : 16=1 : 8
Perbandingan H : O dalam H2O2=2 : 32=1 : 16
Dalam hidrogen yang sama massanya dapat bersenyawa dengan oksigen yang massanya berbanding sebagai 8 :16 atau 1 : 2
4. Hukum perbandingan volume (hukum Gay –Lussac) : volume gas-gas yang bereaksi dan gas-gas hasil reaksi jika diukur pada suhu dan tekanan yang sama berbanding sebagai bilangan bulat dan sederhana.
contoh :
Gas pentana C5H12 yang mempunyai volume 2 liter dibakar sempurna menurut reaksi :
C5H12 + 8 O2 ⇒ 5 CO2 + 6 H2O
Tentukan volume gas oksigenyang dibutuhkan dan volume gas karbondioksida serta uap air yang terbentuk!
Jawab :
Perbandingan koefisien C5H12 : O2 :CO2 : H2O=1 : 8: 5 : 6, maka
Volume O2 yangdibutuhkan=8/1 x 2 liter=16 liter
Volume CO2 yang terbentuk=5/1 x 2 liter=10 liter
Volume H2O yang terbentuk=6/1 x 2 liter=12 liter
5. Hipotesis Avogadro : pada suhu dan tekanan yang sama, semua gas yang memiliki volume sama akan mengandung jumlah molekul yang sama.
contoh:
Jika diketahui uap air bervolume 250 ml, tentukanlah jumlah mol uap air tersebut pada keadaan dimana gas karbon dioksida bermassa 2,2 gram mempunyai volume 500 ml.
Jawab :
6. HukumBoyle – Gay Lussac : hasil kali tekanan gas dan volume gas akan selalu tetap jika dibagi suhu mutlak.
Massa Atom Relatif dan Massa MolekulRelatif
1. Massa atom dapat ditentukan dengan alat spectrometer massa. Hasil pembacaan spectrometer massa disebut spektrografmassa.
2. Satu satuanmassa atom (1 sma) : massa suatu partikel yang nilainya sebesar 1,67 x 10-7kg.
3. Massa satu atom C-12 adalah 12 sma.
4. Massa atom relatif (Ar) adalah massa rata-ratasuatu atom relative (dibandingkan) dengan 1/12 kali massa atom C-12.
 |
| rumus 1 |
5. Massa atom relatif dari isotop-isotop di alam. Di alam, suatu unsur bisa didapatkan dalam dua jenis atau bahkan lebih isotop. Rumus menentukan atom relatifnya adalah :
 |
| rumus 2 |
6. Massa molekul relatif (Mr) merupakan jumlah massa atom relatif dari seluruh atom penyusun suatu molekul.
Persamaan Reaksi
1. Persamaan reaksi : cara memberikan lambang bagi suatu perubahan kimia (reaksi kimia). Persamaan reaksi menggambarkan rumus kimia zat-zat pereaksi dan zat-zat hasil reaksi.
2. Zat Perekasi (reaktan) :zat-zat yang mengalami perubahan dalam reaksi kimia.
3. Zat hasil reaksi (produk) :zat-zat hasil perubahan dalam reaksi kimia.
Perhitungan Kimia
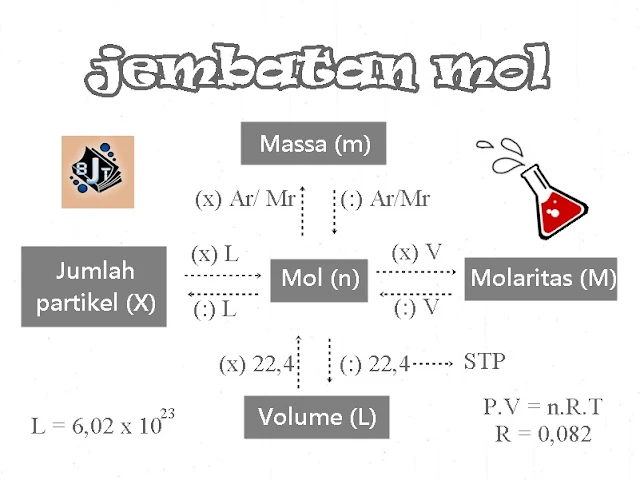 |
| Jembatan mol |
1. Satu mol suatu zat : sejumlah partikel yang terkandung dalam suatu zat yang jumlahnya sama dengan 6,02 x 1023 partikel.
2. Tetapan Avogadro (L) : bilangan yang digunakan untuk menyatakan jumlah partikel satu mol zat yaitu 6,02 x 1023 partikel.
3. Massa molar : massa yang dimiliki oleh 1mol zat yang sama dengan massa atom relative atau massa rumus relatif zat tersebut dan dinyatakan dalam gram per mol.
4. Volume molar gas menyatakan volume yang ditempati satu mol gas pada suhu dan tekanan tertentu. Volume molar gas tidak tergantung pada jenisnya, tetapi pada jumlah mol, suhu dan tekanan pengukuran.
5. Standard Temperature Pressure (STP) : keadaan gas pada suhu 0oC dan tekanan 1 atmosfer. Pada STP, volume molar gas sama dengan 22,4 L/mol.
6. Room Temperature Pressure (RTP) : keadaangas pada suhu 25oC dan tekanan 1 atmosfer. Pada RTP, volume molar gas sama dengan 24,4 L/mol.
7. Kemolaran zat menyatakan jumlah mol zat terlarut dalam tiap liter larutan.
8. Pereaksi pembatas : pereaksi yang habis bereaksi terlebih dahulu dalam suatu reaksi kimia.
9. Rumus empiris : perbandingan paling sederhana dalam komposisi suatu senyawa.
Rumus molekul adalah kelipatan dari rumus empiris.
10. Hidrat : zat padat yang mengikat beberapamolekul air sebagai bagian dari struktur kristalnya.
contoh : CuSO4.5H2O,FeSO4.7H2O dan lain sebagainya.
Langkah-langkah Penyelesaian Perhitungan Kimia
1. Menuliskan persamaan reaksi lengkap dengan koefisien yang tepat.
2. Menghitung mol zat dari data yang diketahui dengan rumus yang sesuai.
3. Menentukan pereaksi pembatas berdasarkan perbandingan koefisien reaksi
4. Menentukan mol zat yang ditanyakan berdasarkan pada perbandingan koefisien reaksi.
5. Jawab pertanyaan dengan menggunakan molzat yang telah dicari pada tahap di atas.
contoh :
Sejumlah 3,2 gramgas metana (CH4) dibakar dengan 16 gram gas oksigen. Berapa massa gas karbon dioksida yang terbentuk?
jawab :
1. Persamaan reaksi
CH4 + 2 O2 ⇒ CO2 + 2 H2O
2. Mol zat yang diketahui
nCH4=massa/Mr =3,2/(12+4) =0,2 mol
nO2= massa/Mr = 16/(2.16) =0,5 mol
3. Perbandingan koefisien dari persamaan reaksi (no.1)
CH4: O2 : CO2 : H2O=1 : 2 : 1 : 2
CH4=0,2 mol/1 =0,2 mol
O2= 0,5 mol/2=0,25 mol
hasil pembagian CH4 lebih kecil dari O2 , maka CH4 adalah pereaksi pembatas
4. Mol zat yang ditanyakan
nCO2=1/1 x 0,2 mol=0,2 mol
5. Jawab pertanyaan
massaCO2=n x Mr
=0,2 mol x (12+2(16))
=0,2 x 44
=8,8 gram
https://www.radarhot.com/2018/05/stoikiometri-hukum-hukum-dasar-kimia-1.html
Turunan Fungsi by Bimbel Jakarta Timur
Sebelum ke Rumus-Rumus, Contoh Soal dan Pembahasan Bimbel Jakarta Timur menjabarkan definisi secara Matematika, Fisika, Ekonomi dan Rekayasa
Dalam matematika
Turunan fungsi adalah konsep yang terkait dengan perubahan suatu fungsi terhadap variabel independennya. Dalam istilah yang lebih sederhana, turunan memberikan informasi tentang sejauh mana suatu fungsi berubah ketika nilai variabel independennya berubah. Turunan sering digunakan untuk mengukur kecepatan perubahan suatu fungsi pada suatu titik tertentu.
Interpretasi geometris dari turunan adalah sebagai gradien atau kemiringan garis singgung pada kurva fungsi pada titik tertentu. Turunan memberikan informasi tentang kecepatan perubahan nilai fungsi terhadap perubahan nilai variabel independennya.
Beberapa aturan turunan yang umum digunakan melibatkan aturan pangkat, aturan rantai, dan aturan jumlah/diferensiasi.
Dalam fisika
Turunan fungsi sering digunakan untuk menyatakan hubungan antara berbagai variabel dan untuk mengukur sejauh mana suatu besaran fisika berubah terhadap waktu atau variabel lainnya. Beberapa konsep turunan fungsi yang umum digunakan dalam fisika melibatkan kecepatan, percepatan, dan laju perubahan suatu besaran terhadap besaran lainnya.
Konsep turunan ini memberikan cara matematis untuk menggambarkan perubahan atau laju perubahan dalam berbagai fenomena fisika. Turunan seringkali memainkan peran penting dalam pembentukan persamaan diferensial yang menggambarkan perilaku sistem fisika.
Dalam ekonomi
Turunan fungsi digunakan untuk menyatakan hubungan antara berbagai variabel ekonomi dan untuk mengukur perubahan suatu besaran ekonomi terhadap variabel lainnya. Beberapa contoh penggunaan turunan dalam ekonomi melibatkan konsep elastisitas, produksi, dan utilitas.
Konsep turunan membantu para ekonom untuk memahami respons sistem ekonomi terhadap perubahan dalam variabel-variabel kunci dan mengukur dampak perubahan tersebut pada keputusan ekonomi. Ini memungkinkan ekonom untuk mengambil keputusan yang lebih informasional dan mendalam dalam menganalisis fenomena ekonomi.
Dalam rekayasa
Turunan fungsi sangat penting karena membantu insinyur untuk memahami dan mengoptimalkan berbagai fenomena fisika atau matematika yang muncul dalam perancangan dan analisis sistem rekayasa. Beberapa aplikasi turunan dalam rekayasa melibatkan analisis sinyal, kontrol sistem, optimisasi, dan permodelan sistem fisik. Berikut adalah beberapa contoh penggunaan turunan dalam rekayasa:
1. Analisis Sinyal (Signal Analysis):
- Dalam pemrosesan sinyal, turunan sering digunakan untuk menganalisis karakteristik sinyal. Turunan sinyal dapat memberikan informasi tentang frekuensi, amplitudo, dan fase.
2. Kontrol Sistem (Control Systems):
- Dalam analisis dan desain sistem kontrol, turunan sering digunakan untuk mengukur laju perubahan suatu variabel terhadap waktu. Misalnya, turunan posisi terhadap waktu memberikan kecepatan, dan turunan kecepatan memberikan percepatan.
3. Optimisasi (Optimization):
- Dalam masalah optimisasi, turunan digunakan untuk menemukan nilai minimum atau maksimum suatu fungsi. Turunan pertama dan kedua sering digunakan dalam analisis titik stasioner (titik kritis) untuk menentukan apakah suatu solusi merupakan minimum, maksimum, atau titik saddle.
4. Permodelan Dinamis Sistem Fisik:
- Turunan berperan penting dalam permodelan matematis sistem fisik yang dinamis, seperti persamaan gerak dalam mekanika atau hukum-hukum dasar elektronika.
5. Pemrosesan Citra (Image Processing):
- Dalam pemrosesan citra, turunan dapat digunakan untuk mendeteksi tepi atau perubahan intensitas dalam citra.
6. Analisis Struktur (Structural Analysis):
- Dalam analisis struktur, turunan digunakan untuk menghitung momen, tegangan, dan deformasi dalam elemen struktural. Turunan juga digunakan dalam permodelan respons dinamis struktur terhadap beban dinamis.
7. Analisis Perpindahan Panas (Heat Transfer Analysis):
- Dalam analisis perpindahan panas, turunan digunakan untuk menghitung gradien suhu dan menggambarkan distribusi panas dalam suatu sistem.
8. Analisis Sistem Elektromagnetik:
- Dalam analisis sistem elektromagnetik, turunan digunakan untuk memodelkan hubungan antara medan elektromagnetik dan sirkuit listrik.
Turunan juga terlibat dalam pembuatan model matematis sistem dan memainkan peran penting dalam analisis numerik untuk memecahkan persamaan diferensial dan permasalahan matematika lainnya yang muncul dalam rekayasa. Oleh karena itu, pemahaman yang kuat tentang konsep turunan sangat penting bagi insinyur rekayasa.
y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :
A. Definisi
Untuk y adalah fungsi dari x atau y=f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y=f(x) terhadap x didefinisikan sebagai :
Contoh :
Jika f (x)=x2 – 3x, maka turunan fungsi f (x)adalah
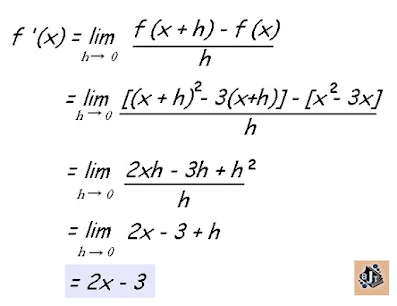 |
| Rumus 2 |
B. Rumus Dasar Turunan
- · Turunan fungsi konstan k. Jika f(x)=k, maka f ‘(x)=0
- · Jika f(x)=ax, maka f ‘(x)=a
- · Jika f(x)=axn, maka f ‘(x)=anxn-1
- · Jika f(x)=u(x) + v(x), maka f ‘(x)=u’(x) + v’(x)
- · Jika f(x)=u(x) . v(x), maka f ‘(x)=u’(x) .v(x) + v’(x) . u(x)
v(x)
maka f ‘(x)= u’(x) . v(x) + v’(x) . u(x)
[v(x)]²
· 7. Jika f(x)=[u(x)]n, maka f‘(x)=n [u(x)]n-1.u’(x)
· 8. Turunan fungsi komposisi (dalil rantai)
Jika y=f(g(x)), maka =dy = dy .dg
dx dg dx
TURUNAN FUNGSI TRIGONOMETRI
- Jika f(x)=sin x, maka f’(x)=cos x
- Jika f(x)=cos x, maka f’(x)=-sin x
- Jika f(x)=tan x, maka f’(x)=sec2x
PERSAMAAN GARIS SINGGUNG DAN GARIS NORMAL KURVA
- · Gradien garis singgung kurva di titik (x1,y1)pada kurva f(x) adalah m=f’(x1)
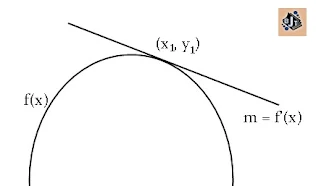 |
| Gradien |
Persamaan garis singgung kurva
y – y1=m (x – x1)
·
- Garis normal kurva adalah suatu garis yang tegaklurus dengan garis singgung kurva di titik yang sama dengan titik singgungkurva.
 |
| Kurva |
· Gradiengaris normal kurva di titik (x1,y1) pada kurva f(x)
a adalah mn=-1/f'(x)
· Persamaan garis normal kurva
y – y1=mn (x – x1)
FUNGSI NAIK, FUNGSI TURUN DAN NILAI STASIONER
- · Fungsi naik
Suatu fungsi dikatakan naik dalam suatuselang untuk x1 < x2 maka f(x1) < f(x2)
kurva naik jika f’(x) > 0
- · Fungsi turun
Suatu fungsi dikatakan turun dalam suatuselang untuk x1 < x2 maka f(x1) > f(x2)
kurva naik jika f’(x) < 0
- · Nilai dan titik stasioner
Jika fungsi f(x) mempunyai turunan pada x=a dan f’(a)=0, maka f(a) merupakan nilai stasioner fungsi f(x)
Jika f’(a)=0, maka titik stasioner fungsiadalah (a, f(a))
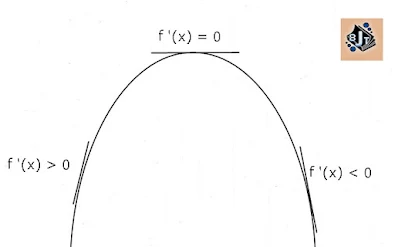
· Jenis nilai stasioner dimana f”(x) adalahturunan kedua fungsi f(x)
Jika f”(a) < 0, maka f(a) berjenismaksimum
 |
| Kurva 2 |
Jika f”(a) > 0, maka f(a) berjenis minimum
 |
| Kurva 3 |
Jika f”(a)= 0, maka (a, f(a)) adalah titik belok
 |
| Kurva 4 |
CONTOH SOAL DAN PEMBAHASAN
1. Turunan pertama dari fungsi f(x)=4x3 -3x2 + 8x -5 adalah….
Pembahasan:
f’(x) =4.3.x3-1 – 3.2.x2-1+ 8.1 x1-1 -5.0.x0-1
=12x2 – 6x1 + 8x0 – 0
=12x2 – 6x + 8
Pembahasan:
misal u(x)=3x2 +2, u’(x)=6x
v(x)=2x -5, v’(x)=2
maka y’=u’(x) . v(x) + v’(x) . u(x)
=6x (2x – 5) + 2 (3x2+2)
=12x2 – 30 x + 6 x2+ 4
=18x2 – 30x + 4
3. Turunan pertama dari dari y=(5x2 +3 x)3adalah…
Pembahasan:
misal u(x)=(5x2 +3x), u’(x)=10x + 3
y=[u(x)]n, maka y' =n [u(x)]n-1.u’(x)
= 3(5x2 +3x)2(10x + 3)
= (30x + 9)(5x2 +3x)2
1. 4. Turunan pertama dari fungsi y=∛(6x+5) adalah…
Pembahasan:
y=(6x + 5)1/3,u(x)=6x=5, u’(x)=6
y’=1/3 (6x + 5)-2/3(6)
=2(6x + 5)-2/3
= 2
∛(6x+5)²
5. Turunan pertama dari fungsi f(x)=3x + 2 adalah…
x - 1
Pembahasan:
u(x)=3x+2, u’(x)=3
v(x)=x-1, v’(x)=1
maka f ‘(x)= u’(x) . v(x) - v’(x) . u(x)
[v(x)]²
=3(x-1) - 1(3x+2)
(x-1)²
= -5
(x-1)²
6. Persamaan garis singgung para bola y=x2+ 4x -5
pada titik (-1,2) adalah…
Pembahasan:
y’=2x + 4
m=2(-1) + 4=2
persamaan garis singgung
y – 2=2 (x –(-1))
y – 2=2x + 2
y=2x + 4
2 7. Persamaan garis normal kurva y=x3-4x2+ 5x-2
pada titik (2,-5) adalah…
Pembahasan:
y’=3x2- 8x + 5=3(2)2– 8(2) + 5=1
mn=-1/y’=-1/1=-1
persamaan garis normal
y – (-5)=-1(x-2)
y + 5=-x + 2
y=-x -7
8. 8. Fungsi f(x)=x2 – 9x naik pada interval…
Pembahasan:
fungsi naik jika f’(x) > 0 ,
maka 2x –9 > 0
jadi fungsi naik pada x > 4,5
9. 9. Tentukan nilai stasioner dari fungsi f(x)=2x3 – 15x2 +36x – 10 !
Pembahasan:
titik stasioner dicapai jika f’(x)=0
6x2 -30x + 36=0
6 (x -2) (x-3)=0
x1=2, x2=3
Nilai stasioner didapat
f(2)=18 dan
f(3)=17
10. Tentukan turunan pertama dari y=sin³(2x+3)
Pembahasan :
y'=3sin²(2x+3).cos(2x+3) (2)
=6sin²(2x+3).cos(2x+3)
https://www.radarhot.com/2018/03/turunan-fungsi.html
Mengenal Bahasa Pemrograman VBNET By Bimbel Jakarta Timur
Bimbel Jakarta Timur mencoba mengenalkan Bahasa Pemrograman VB.net yaitu (Visual Basic .NET) adalah bahasa pemrograman berorientasi objek yang dikembangkan oleh Microsoft. Sebagai penerus dari Visual Basic (VB), VB.NET didesain untuk bekerja sepenuhnya dengan .NET Framework, sebuah platform pengembangan perangkat lunak yang luas. Berikut adalah beberapa poin kunci yang menjelaskan VB.NET secara singkat:
1. Berorientasi Objek: VB.NET adalah bahasa berorientasi objek (OOP) yang mendukung konsep seperti kelas, objek, enkapsulasi, pewarisan, dan polimorfisme.
2. Integrasi dengan .NET Framework: Sepenuhnya terintegrasi dengan .NET Framework, memanfaatkan library dan alat yang disediakan untuk membangun berbagai jenis aplikasi.
3. Kemudahan Penggunaan: Dirancang dengan fokus pada kemudahan penggunaan, mewarisi beberapa konsep dan sintaks dari pendahulunya, Visual Basic. Ini membuatnya mudah dipahami, terutama bagi pemula.
4. Lingkungan Pengembangan Terpadu (IDE): VB.NET umumnya digunakan dalam lingkungan pengembangan terpadu (IDE) Microsoft Visual Studio. Visual Studio menyediakan alat pengembangan lengkap dan efisien.
5. Dukungan Pengembangan Aplikasi Beragam: VB.NET digunakan untuk mengembangkan aplikasi desktop Windows, aplikasi web ASP.NET, layanan web, dan aplikasi perangkat seluler.
6. Bahasa Terstruktur: Mendukung pemrograman terstruktur dan bersifat strongly-typed, memerlukan deklarasi eksplisit untuk tipe data variabel.
7. Pilihan Populer di Platform Microsoft: VB.NET telah menjadi pilihan yang populer di kalangan pengembang untuk proyek-proyek yang berfokus pada platform Microsoft, terutama karena kemudahan penggunaannya dan integrasinya dengan ekosistem .NET.
8. Kompatibilitas Mundur dengan Visual Basic: Meskipun ada perubahan signifikan dari Visual Basic ke VB.NET, ada upaya untuk memastikan kompatibilitas mundur sehingga kode Visual Basic yang sudah ada dapat dimigrasikan dengan relatif mudah.
Dengan kelebihan kemudahan penggunaan dan integrasi yang solid dengan teknologi Microsoft, VB.NET tetap menjadi pilihan yang valid untuk pengembangan aplikasi di ekosistem Microsoft.
Instalasi VB.NET melibatkan penggunaan Microsoft Visual Studio, lingkungan pengembangan terpadu (IDE) yang menyediakan dukungan penuh untuk VB.NET dan platform .NET secara umum. Berikut adalah langkah-langkah umum untuk menginstal VB.NET dengan menggunakan Microsoft Visual Studio:
1. Unduh Visual Studio:
- Kunjungi situs resmi Visual Studio di [https://visualstudio.microsoft.com/](https://visualstudio.microsoft.com/).
- Pilih edisi Visual Studio yang sesuai dengan kebutuhan Anda (misalnya, Visual Studio Community Edition untuk pengembang perseorangan).
- Klik tombol "Unduh" untuk mengunduh installer Visual Studio.
2. Jalankan Installer:
- Buka file installer yang telah diunduh.
- Ikuti petunjuk pada layar untuk memulai proses instalasi.
3. Pilih Komponen:
- Selama proses instalasi, Anda akan diminta untuk memilih komponen yang ingin diinstal. Pastikan untuk memilih "Visual Basic" dan "Cross-platform .NET development" atau komponen yang relevan untuk pengembangan VB.NET.
4. Instalasi Tambahan (Opsional):
- Pada beberapa titik, Anda mungkin diminta untuk menginstal komponen tambahan atau memilih pengaturan khusus. Sesuaikan instalasi sesuai kebutuhan Anda.
5. Registrasi dan Login:
- Saat diminta, lakukan registrasi atau login menggunakan akun Microsoft. Jika Anda belum memiliki akun, Anda dapat membuatnya selama proses instalasi.
6. Proses Instalasi:
- Lanjutkan dengan membiarkan installer menyelesaikan proses instalasi. Ini mungkin memerlukan beberapa waktu tergantung pada kecepatan koneksi internet dan spesifikasi sistem komputer Anda.
7. Mulai Visual Studio:
- Setelah instalasi selesai, buka Microsoft Visual Studio dari menu Start atau dengan mengklik ikonnya di desktop.
8. Aktivasi (Jika Diperlukan):
- Jika Anda menggunakan edisi yang memerlukan aktivasi (seperti Visual Studio Community Edition), Anda mungkin diminta untuk mengaktifkannya menggunakan akun Microsoft.
Setelah langkah-langkah ini diselesaikan, Visual Studio akan siap digunakan untuk pengembangan VB.NET. Anda dapat membuat proyek baru, mengelola solusi, dan mulai menulis dan menguji kode VB.NET Anda. Pastikan untuk selalu merujuk ke dokumentasi resmi Visual Studio dan VB.NET untuk informasi lebih lanjut dan panduan terperinci.
Contoh sederhana dari program VB.NET yang mencetak "Hello, World!" ke konsol:
```vbnet
Module HelloWorld
Sub Main()
' Menampilkan pesan "Hello, World!" di konsol
Console.WriteLine("Hello, World!")
' Menunggu agar konsol tidak langsung ditutup
Console.ReadLine()
End Sub
End Module
```
Dalam program ini:
- `Module HelloWorld` adalah modul utama yang mengandung program.
- `Sub Main()` adalah subroutine yang dijalankan saat program dimulai. Itu adalah titik awal eksekusi.
- `Console.WriteLine("Hello, World!")` mencetak teks "Hello, World!" ke konsol.
- `Console.ReadLine()` digunakan untuk menahan konsol agar tidak langsung tertutup sehingga Anda dapat melihat hasil keluaran.
Program ini adalah contoh sederhana untuk memahami sintaks dasar VB.NET dan cara menggunakan konsol untuk output. Anda dapat menyimpannya dalam file dengan ekstensi `.vb`, dan kemudian mengkompilasi dan menjalankannya menggunakan Visual Studio atau melalui Command Prompt dengan menggunakan perintah `vbc` (Visual Basic Compiler).
Menunjukkan penggunaan variabel, percabangan (if-else), dan pengulangan (loop):
```vbnet
Module ComplexExample
Sub Main()
' Deklarasi variabel
Dim nilai As Integer
Dim pesan As String
' Input nilai dari pengguna
Console.Write("Masukkan nilai: ")
nilai = Integer.Parse(Console.ReadLine())
' Percabangan if-else
If nilai >= 70 Then
pesan = "Selamat! Anda lulus."
Else
pesan = "Maaf, Anda belum lulus."
End If
' Menampilkan pesan
Console.WriteLine(pesan)
' Pengulangan for
Console.WriteLine("Mencetak angka 1 sampai 5:")
For i As Integer = 1 To 5
Console.Write(i & " ")
Next
' Menunggu agar konsol tidak langsung ditutup
Console.ReadLine()
End Sub
End Module
```
Dalam program ini:
- `Dim nilai As Integer` dan `Dim pesan As String` digunakan untuk mendeklarasikan variabel `nilai` dan `pesan`.
- `Console.Write("Masukkan nilai: ")` digunakan untuk menampilkan pesan ke pengguna dan mengambil input nilai dari pengguna.
- `If nilai >= 70 Then ... Else ... End If` adalah struktur percabangan yang mengevaluasi apakah nilai lebih besar atau sama dengan 70, dan menentukan pesan yang akan ditampilkan.
- Pengulangan `For i As Integer = 1 To 5` digunakan untuk mencetak angka dari 1 sampai 5.
Program ini memberikan gambaran tentang penggunaan variabel, percabangan, dan pengulangan dalam VB.NET. Anda dapat menyimpannya dalam file dengan ekstensi `.vb`, dan kemudian mengkompilasi dan menjalankannya menggunakan Visual Studio atau melalui Command Prompt dengan menggunakan perintah `vbc` (Visual Basic Compiler).
Program ini melibatkan penggunaan fungsi, array, pengulangan, dan beberapa konsep dasar pemrograman lainnya:
```vbnet
Module AdvancedExample
Sub Main()
' Memanggil fungsi untuk menghitung luas dan keliling lingkaran
Dim radius As Double = 5.0
Dim area As Double = HitungLuasLingkaran(radius)
Dim circumference As Double = HitungKelilingLingkaran(radius)
' Menampilkan hasil
Console.WriteLine("Lingkaran dengan radius {0} memiliki luas {1} dan keliling {2}", radius, area, circumference)
' Membuat array dan menampilkan elemennya
Dim numbers() As Integer = {1, 2, 3, 4, 5}
Console.Write("Elemen array: ")
For Each number As Integer In numbers
Console.Write(number & " ")
Next
' Menampilkan deret Fibonacci
Console.WriteLine(vbCrLf & "Deret Fibonacci pertama:")
For i As Integer = 0 To 9
Console.Write(Fibonacci(i) & " ")
Next
' Menunggu agar konsol tidak langsung ditutup
Console.ReadLine()
End Sub
' Fungsi untuk menghitung luas lingkaran
Function HitungLuasLingkaran(radius As Double) As Double
Return Math.PI * Math.Pow(radius, 2)
End Function
' Fungsi untuk menghitung keliling lingkaran
Function HitungKelilingLingkaran(radius As Double) As Double
Return 2 * Math.PI * radius
End Function
' Fungsi untuk menghasilkan deret Fibonacci
Function Fibonacci(n As Integer) As Integer
If n <= 1 Then
Return n
Else
Return Fibonacci(n - 1) + Fibonacci(n - 2)
End If
End Function
End Module
```
Dalam program ini:
- Terdapat dua fungsi, `HitungLuasLingkaran` dan `HitungKelilingLingkaran`, yang digunakan untuk menghitung luas dan keliling lingkaran berdasarkan radius.
- Program juga membuat dan menampilkan elemen-elemen dalam sebuah array.
- Ada fungsi `Fibonacci` yang menghasilkan deret Fibonacci hingga suku ke-9.
Program ini memberikan gambaran tentang penggunaan fungsi, array, dan beberapa konsep lainnya dalam VB.NET. Anda dapat menyimpannya dalam file dengan ekstensi `.vb` dan menjalankannya menggunakan Visual Studio atau melalui Command Prompt dengan menggunakan perintah `vbc` (Visual Basic Compiler).